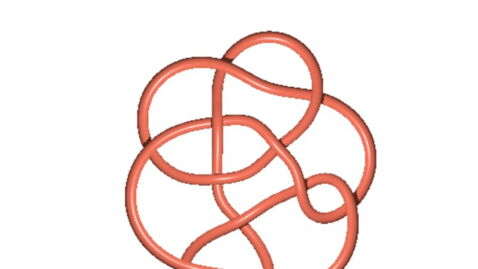
For more than fifty years, mathematicians have disagreed about a rather complex problem known as the 'Conway knot' which even decorates the doors of the Isaac Newton Institute for Mathematical Sciences at the prestigious University of Cambridge.
Discover our latest podcast

Quanta revealed in May that a young graduate from the University of Texas, Lisa Piccirillo, managed to discover the secret and in less than a week no less. Not long after, her revelation was published in the Annals of Mathematics.
Is this knot 'slice'?
This problem was one of the long-standing mysteries of knot theory, a field of topology. The discipline is not only useful in the world of mathematics but has also helped to improve researchers' understanding of the potential shape of the Universe or the shape of DNA, for example.
But what is it more specifically? As it turns out, in mathematics, a knot is similar to a simple physical knot, with the one notable difference that its two ends are connected to each other. These knots in question resemble tangled loops since they have no ends.
The Conway knot, in particular, is a mathematical knot with 11 crossings which was discovered by the scientist with the same name, John Horton Conway. Until this year, the long-standing question was, to put it simply, whether this knot was 'slice'. In knot theory, a knot is an embedded circle in a 3-sphere which can be thought of as the boundary of a 4-dimensional ball. A knot is slice if it bounds a nicely embedded 2-dimensional disk in the 4-dimensional ball.
The “twin” solution
Many knots are “slices”. Conway's knot was, however, the last with 11 crossings of the thousands of existing knots whose nature mathematicians did not know. Lisa Piccirillo has therefore finally managed to find an answer to this complex problem.
In order to solve this problem, she relied on the fact that certain knots have “mutant siblings”, whose crossings are reversed like a kind of mirror effect. However, they have the same nature: if one is "slice", then the other has to be as well. Therefore, she redrew the knot in a method called making its trace because if this sibling knot proved to be slice, the Conway knot would be as well. And as it finally turned out, this knot was not "slice".
If you want to find out more about how she solved this fifty-year-old riddle, check out Quanta magazine for all the details.